One Compartment Model
Table of Contents
- 1 Description
- 2 Usage
- 3 Arguments
- 4 Return value
- 5 Note
1 Description
Function pmx_solve_onecpt solves a one-compartment PK
model (Figure 1). The model obtains the mass \((y_1, y_2)\) in each compartment
by solving the ordinary differential equations(ODEs)
\begin{align}\label{eq:onecpt}
y_1' &= -k_a y_1, \\\
y_2' &= k_a y_1 - \left(\frac{CL}{V_2} + \frac{Q}{V_2}\right) y_2.
\end{align}
The plasma concentrations of parent drug in the central compartment can then be calculated as \(c=y_2/V_2\).
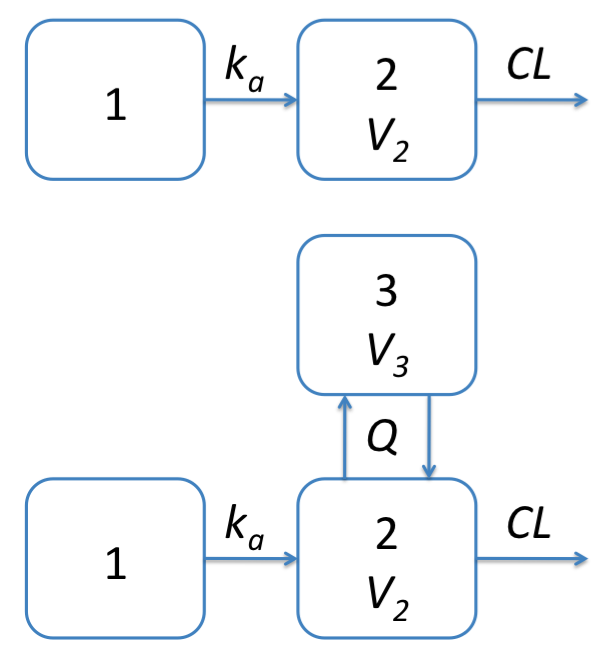
Figure 1: One and two compartment models with first order absorption implemented in Torsten.
2 Usage
matrix = pmx_solve_onecpt(time, amt, rate, ii, evid, cmt, addl, ss, theta [, biovar, tlag ] )
3 Arguments
See Tables in Section Events specification.
4 Return value
An ncmt-by-nt matrix, where nt is the number of time steps and ncmt=2 is the number of compartments.
5 Note
- ODE Parameters
thetashould consist of \(CL\), \(V_2\), \(k_a\), in that order. biovarandtlagare optional, so that the following are allowed:
pmx_solve_onecpt(..., theta);
pmx_solve_onecpt(..., theta, biovar);
pmx_solve_onecpt(..., theta, biovar, tlag);
- Setting \(k_a = 0\) eliminates the first-order absorption.